?看點?? ?今年中考數學,引起了大眾不少關注。回歸試卷,眾多考生沒有拿下的最后一題,“難”在哪里?值得關注的是,這些題目完全回歸課本,沒有一點超綱考查,卻非常靈活。這些不套路的題目,對于我們今后小初高階段的數學學習,又會有怎樣的啟發呢?
文丨魚圈教研團? ? 編丨袁梓曦
截至我們發稿前,全國各地大部分地區都已經結束中考。和高考一樣,考試結束網上最先討論的就是“今年考得難不難”這樣的話題。
根據網上的消息,我們大概捋了一下:
北京、上海、江蘇、重慶,安徽、青島的考生普遍覺得偏難;
浙江考生覺得沒那么難但全做出的人也不多。
整體來說,今年中考的數學不簡單。
不過,難易這種事,因人而異,網上的調查也僅限于當事人觀感,咱們還是就事論事,把考卷拿來做一遍再評判。
2024年中考落下帷幕
數學又“難”又“簡單”
我們一般說數學考得難,指的是試卷最后一題難度,比如填空、選擇最后一題,最常見是看整張試卷最后一題的難度。
普娃和牛娃的差距,或者說最后孩子是去普高還是重高,很大程度上要看這種題目能不能做出來。
因為該類題目分值比較高,如果沒思路,那光一道題就能拉開10分左右的差距。在中考,也許志愿就得從上一檔滑落到下一檔了。
那我們具體來看一下這幾個省市中考數學的最后一道大題。
北京最后一題,把函數和幾何放在一起:
上海最后一題,幾何題:

重慶最后一題,幾何題:
浙江最后一題,幾何題:
我們做了下這幾道題,感覺論“知識點”不難,因為解題中用到的都是課本內的知識,而且是非常基礎的概念和定理。
那考生反饋的“難”是落在哪里呢?
我們認為,是因為這些題目非常不套路。
知識點還是那些知識點,但考查的深度和靈活度和“刷的題”太不一樣了!
我們就以沒那么難的浙江卷為例,解題步驟不復雜:
本題在圓中內接了四邊形,研究線與圓中四邊形基本元素之間的關系:
這幾個知識點之間不獨立,環環相扣。
只有真正理解概念和定理,而不是單純考記憶背出一些公式,才能在碰到這種題目時不慌不亂,抽絲剝繭,順利下筆。
從前刷題強調的解題技巧,現在都用不上了,只有重視數學概念、原理以及法則之間的聯系,理解透徹了,題也就不難了。
中考滿分的秘密——幾何
小學階段能做些什么
從上面分析可以看出,這些省市的最后一題一般都會選擇幾何題,或者把幾何和函數結合到一起考查。
我們翻看了往年的中考試卷,的確如此。
那么,對于家長和孩子來說,幾何的學習就得好好琢磨了,特別是想要沖刺滿分,目標“重高”的家庭。
小初高的數學體系可以大致分成三個模塊:代數與計算、幾何和統計與概率。
我們重點看幾何模塊。
小學階段的幾何學習偏認知向:了解點線面、平面圖形、立體圖形的基本特征。
考試也特別簡單,反而在幾何計算中孩子失分的情況會更多一些,比如算周長和面積。
這里家長們要分辨一下,因為小學幾何涉及的周長面積是很“直白”的,更多的是考“代數能力”,比如下面這題
很少有孩子是因為不會正方形、長方形的周長面積公式而錯的。
所以,嚴格意義上,小學階段的幾何學習難度一點都不大。
初中階段,幾何學習要從初二開始:此時才對平面幾何有了深度探究,要能想象、能割補、會添輔助線,這才是真正的幾何入門。
幾何和代數學習不一樣。
做一道幾何題,最重要的就是思考出解題的邏輯線。從已知條件出發,一步一步,嚴謹地推導出結論,完成證明。
而到了高中之后,接觸的就是立體幾何了,在難度上當然又升了一個臺階。不過在高中,會引入一個新的知識點——向量。
當孩子會用空間向量后,很多立體問題其實可以轉為向量問題,那接下來需要的就是代數計算能力,和幾何相關性沒那么大了。
綜合以上分析,我們認為對于幾何學習,最精髓的部分其實是在初中,真正用幾何思維來解幾何問題。
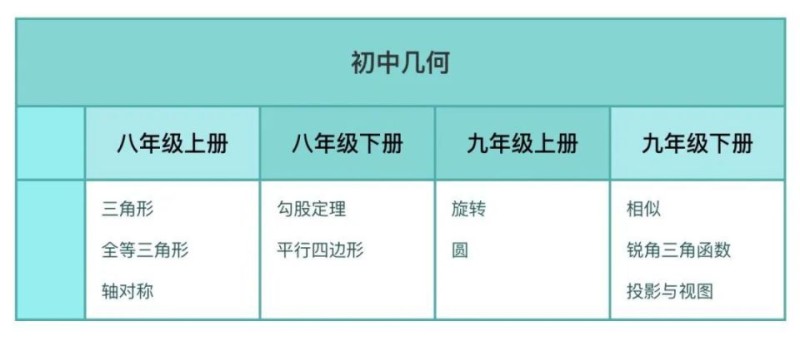
這就難怪,一張中考卷,幾何的分值大概占據40%-45%。
但是在小學階段,幾何學習確實比較淺;那么,對于學有余力的孩子,可以適當給他鋪墊一些幾何認知,這樣銜接到初中幾何會相對順暢。
注意,我們不建議提前去學習初中幾何內容,而是在小學階段重點把幾何的基礎知識和性質好好摸透,搭建孩子的幾何底層能力。
有關「課內」和「課外」的建議如下。
首先,一定要重視課內。
再次強調,小學階段的幾何知識很簡單,但不代表不重要。
尤其是簡單幾何的概念和特征,他們是初高中幾何學習的地基,所有高階的幾何推理都是從一個點、一條線、一個面開始的。
如果孩子只是記住了知識點,而沒有去理解,遇到新題型,比如今年的中高考題目,自然覺得“很難”。
幾何非常重視邏輯性,我們可以讓孩子自己梳理出所學幾何知識的思維導圖;幾何圖形的一個性質到另一個性質是如何被推導出來的,最好都自己證明一遍。
能做到這一步,其實就是在課內學習的基礎上又向下深挖了一步,這個地基打得就越穩。
在課內基礎上,我們推薦做一些拓展。
學有余力的孩子,可以嘗試接觸小奧的幾何體系,一些題目蘊含了不少幾何思維,可以更深刻地理解幾何之間的關系。
特別是它們涉及的原理都是當前校內知識,也就是說,沒有需要超前和額外補充的知識點。
除此之外,家中可以提供一些幾何數學讀物給孩子,比起正兒八經做小奧題,看看書就“無痛”多了吧。
繪本類:《折紙的幾何》《這就是幾何》《DK我的第一本幾何思維》《揭秘幾何》《形狀國的傳說》
故事類:《幾何王國大冒險》《幾何真好玩》
閱讀類:《圖解奧數》《幾何原本》《幾何之美》《不焦慮的幾何》
當然,一些幾何的桌游也是很好的補充,盡量在孩子生活中滲透一些幾何思想。
那么,等孩子上了初中,他可以從容應對幾何的學習和考試。
把中高考數學最后一題放一起看
數學原理和數學思維是關鍵
講完了中考,我們再往前多看一步,把今年高考卷的最后一題一起拿來比較下。
我們主要以新課標Ⅰ卷為例,因為Ⅰ卷參與的省市都是采用新課標的地區,也是教育改革的方向。

2024年數學高考新課標Ⅰ卷最后一題
今年考生普遍反映全國新課標Ⅰ卷最后一題,有點出人意料,考了一道新定義的數列題,屬數論知識,當天考完出來發懵的考生非常多。
學生覺得“發懵”很大概率是因為這種題型完全沒見過,而“數論”在整個小初高學習中都不是重點,只是淺淺接觸了下。
甚至很多孩子都不知道這些知識點屬于數論的范疇,比如整除、余數、進制都是數論里研究的內容。
數論的入門學習在小奧中會有一些,其余就完全是大學才會學到的內容。
因此有挺多博主就開始宣傳,高中要提前讓孩子學高等數學。
按照他們的理論,那孩子要學的東西可太多了,什么“極限與洛必達法則”、“微分中值定理與應用”、“凸凹性與偏導數”、“定積分與應用”……
難道不提前學一些大學知識,就考不好高考了嗎?
不然。
參考人教版高中數學主編章建躍老師的解釋和分析,其實解這題所必需的知識限定完全都在高中課本中。

章建躍:2024高考數學的啟示《回歸課標、重視教材才是王道》
雖然這里構建了一個新情境,但是前兩問只要能讀懂題,理解題目中給出的概念,找到有效信息,就能做。
第三問,有一些難度,構造了新的知識,但是題目中把關于數論的相關知識都告知了,考生需要的就是“依樣畫葫蘆”。
它考查的是考生對新知識的現場理解能力,用數學思維現學現用,高效率地接受新知識并應用。
其實很多國內優質學校的自主招生,很早就開始采用“現學現用”的招生策略,因為這樣可以更客觀地挑選出學習能力強的孩子。
所以,我們認為,高考考到一些沒有學過的知識,本意上不是為了單純鼓勵孩子去超前學;
而是希望通過一道“新題型”來篩選出真正有數學能力的孩子。
這里講的數學能力,可以簡單理解為:
遇到一個新的數學問題,學生可以從自己的“知識庫”中,迅速組建起一套全新的解題邏輯,來應對新問題,而不是拿一個成品化的模具來試著套一套。
即這種能力無法通過反復刷題刷出來。
如此分析,會發現雖然中高考考查的知識點和難度完全不同,但考查方向和邏輯是一致的。
中高考的最后一題絕對不是考學生的“知識量”,它所注重的是“數學能力”。
而構建數學能力背后,需要的是對數學概念原理的理解并應用,即所謂的“數學思維”。
這一點,在孩子今后的數學學習中,是我們需要重點關注的。
發現優質教育



